floodlight.transforms.filter

floodlight.transforms.filter.butterworth_lowpass(xy, order=3, Wn=1, remove_short_seqs=False, **kwargs)

Applies a digital Butterworth lowpass-filter to a XY data object. 1

For filtering, the scipy.filter.butter and the scipy.signal.filtfilt functions are used. This function provides a convenience access to both functions, directly applying the filter to all non-NaN sequences in all columns.

Parameters

• xy (XY) – Floodlight XY Data object.

• order (int, optional) – The order of the filter. Corresponds to the argument N from the scipy. signal.butter function. Default is 3

• Wn (Numeric, optional) – The normalized critical cutoff frequency. Corresponds to the argument Wn from the scipy.signal.butter function. Default is 1.

• remove_short_seqs (bool, optional) – If True, sequences that are to short for the filter with the specified settings are replaced with np.NaNs. If False, they are kept unfiltered. Default is False.

• kwargs – Optional arguments {‘padtype’, ‘padlen’, ‘method’, ‘irlen’} that can be passed to the scipy.signal.filtfilt function.

Returns

xy_filtered – XY object with position data filtered by designed Butterworth low pass filter.

Return type

XY

Notes

The values of the input data are assumed to be numerical. Missing data is assumed to be either np.NaN or None. The Butterworth-filter requires a minimum signal length depending on the settings. A signal is a sequence of data in the XY-object that is not interrupted by missing values. The minimum signal length is defined as \(3 \cdot (order + 1)\). The treatment of signals shorter than the minimum signal length are specified with the remove_short_sequence-argument, where True will replace these sequences with np.NaNs ond False will keep the sequences in the data unfiltered.

Examples

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from floodlight import XY
>>> from floodlight.transforms.filter import butterworth_lowpass

We first generate a noisy XY-object to smooth.

>>> t = np.linspace(-5, 5, 1000)
>>> player_x = np.sin(t) * t + np.random.rand(1000)
>>> player_x[450:495] = np.NaN
>>> player_x[505:550] = np.NaN
>>> player_y = t + np.random.randn()
>>> xy = XY(np.transpose(np.stack((player_x, player_y))), framerate=20)

Apply the Butterworth lowpass filter with its default settings.

>>> xy_filt = butterworth_lowpass(xy)
>>> plt.plot(xy.x)
>>> plt.plot(xy_filt.x, linewidth=3)
>>> plt.legend(("Raw", "Smoothed"))
>>> plt.show()

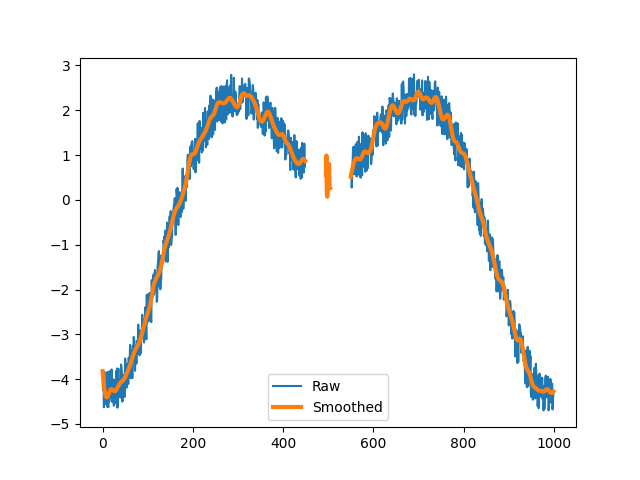
Apply the same filter but remove the sequence that is to short to filter.

>>> xy_filt = butterworth_lowpass(xy, remove_short_seqs=True)
>>> plt.plot(xy.x)
>>> plt.plot(xy_filt.x, linewidth=3)
>>> plt.legend(("Raw", "Smoothed"))
>>> plt.show()

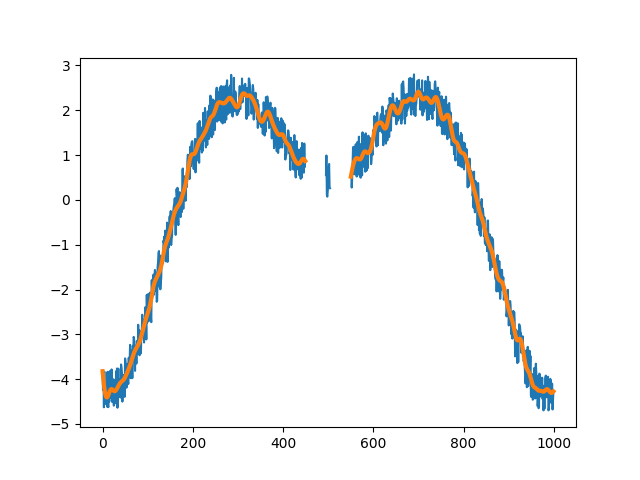
Apply the filter with different specifications.

>>> xy_filt = butterworth_lowpass(xy, order=5, Wn=4)
>>> plt.plot(xy.x)
>>> plt.plot(xy_filt.x, linewidth=3)
>>> plt.legend(("Raw", "Smoothed"))
>>> plt.show()

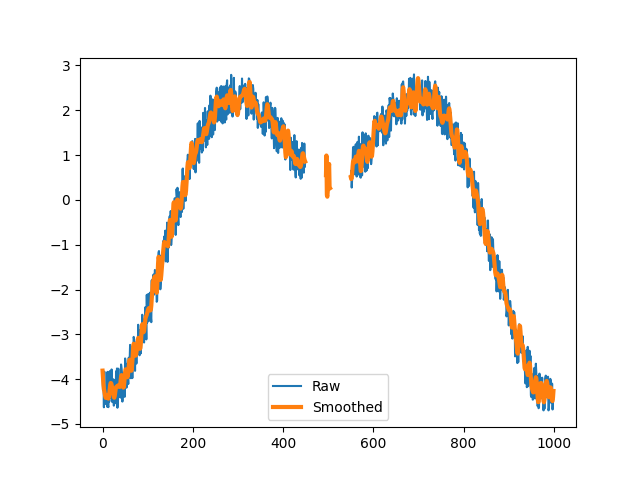
References

1

Butterworth, S. (1930). On the theory of filter amplifiers. Wireless Engineer, 3, 536-541.

floodlight.transforms.filter.savgol_lowpass(xy, window_length=5, poly_order=3, remove_short_seqs=False, **kwargs)

Applies a Savitzky-Golay lowpass-filter to a XY data object. 2

For filtering, the scipy.filter.savgol function is used. This function provides a convenient access to the function, directly applying the filter to all non-NaN sequences in all columns.

Parameters

• xy (XY) – Floodlight XY Data object.

• window_length (int, optional) – The length of the filter window. Corresponds to the argument window_length from the scipy.filter.savgol function. Default is 5.

• polyorder (Numeric, optional) – The order of the polynomial used to fit the samples. poly_order must be less than window_length. Default is 3. Corresponds to the argument polyorder from the scipy.filter.savgol function. Default is 5.

• remove_short_seqs (bool, optional) – If True, sequences that are to short for the Filter with the specified settings are removed from the data. If False, they are kept unfiltered. Default is False.

• kwargs – Optional arguments {‘deriv’, ‘delta’, ‘mode’, ‘cval’} that can be passed to the scipy.signal.savgol function.

Returns

xy_filtered – XY object with position data filtered by designed Butterworth low pass filter.

Return type

XY

Notes

The values of the input data are assumed to be numerical. Missing data is assumed to be either np.NaN or None. The Savitzky-Golay-filter requires a minimum signal length depending on the settings. A signal is a sequence of data in the XY-object that is not interrupted by missing values. The minimum signal length is defined as the window_length. The treatment of signals shorter than the minimum signal length are specified with the remove_short_sequence-argument, where True will replace these sequences with np.NaNs ond False will keep the sequences in the data unfiltered.

Examples

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from floodlight import XY
>>> from floodlight.transforms.filter import savgol_lowpass

We first generate a noisy XY-object to smooth.

>>> t = np.linspace(-5, 5, 1000)
>>> player_x = np.sin(t) * t + np.random.rand(1000)
>>> player_x[450:495] = np.NaN
>>> player_x[505:550] = np.NaN
>>> player_y = t + np.random.randn()
>>> xy = XY(np.transpose(np.stack((player_x, player_y))), framerate=20)

Apply the Savgol lowpass filter with its default settings.

>>> xy_filt = savgol_lowpass(xy)
>>> plt.plot(xy.x)
>>> plt.plot(xy_filt.x, linewidth=3)
>>> plt.legend(("Raw", "Smoothed"))
>>> plt.show()

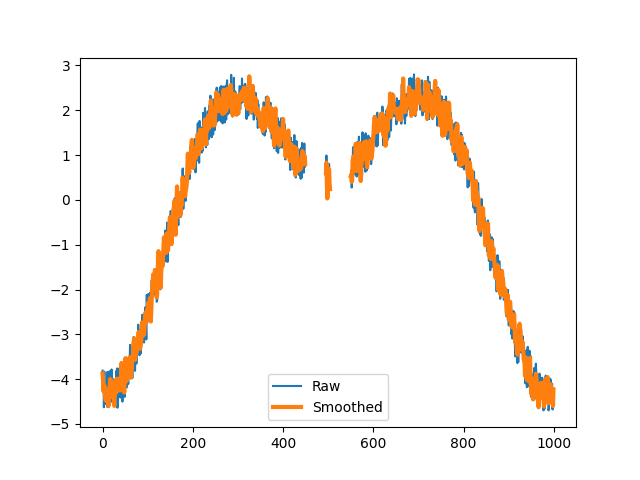
Apply the filter with a longer window lengh and remove the sequence that is to short to filter.

>>> xy_filt = savgol_lowpass(xy, window_length=12, remove_short_seqs=True)
>>> plt.plot(xy.x)
>>> plt.plot(xy_filt.x, linewidth=3)
>>> plt.legend(("Raw", "Smoothed"))
>>> plt.show()

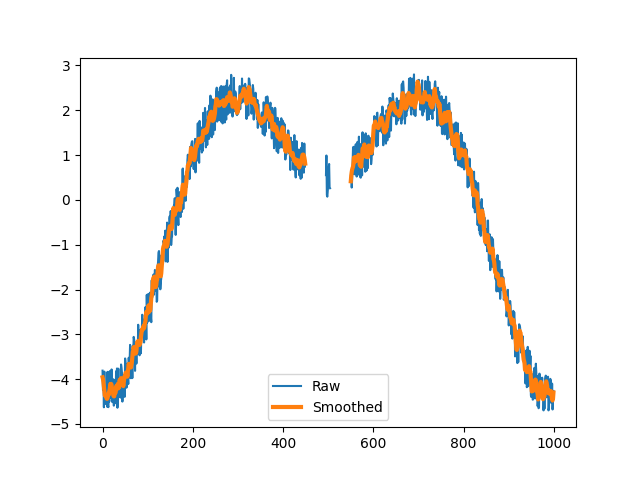
Apply the filter with different specifications.

>>> xy_filt = savgol_lowpass(xy, window_length=50, poly_order=5)
>>> plt.plot(xy.x)
>>> plt.plot(xy_filt.x, linewidth=3)
>>> plt.legend(("Raw", "Smoothed"))
>>> plt.show()

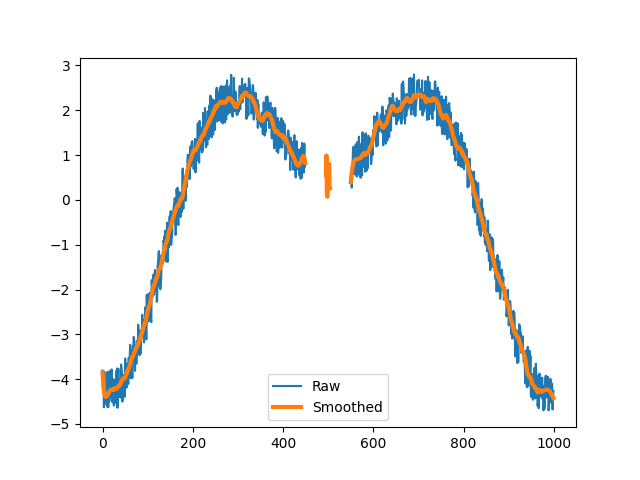
References

2

Savitzky, A.; Golay, M.J. (1964). Smoothing and differentiation of data by simplified least squares procedures. Analytical Chemistry, 36(1), 1627- 1639.